MATH+: MATHEMATIK FÜR DIE ZUKUNFT
Der "Matheagent" am Potsdamer Platz – viele Projekte von MATH+ arbeiten mit sogenannten agentenbasierten Modellierungen. Was das ist, erfährst du im unten verlinkten Interview mit Prof. Dr. Kai Nagel und Dr. Sarah Wolf.
"Mathematik ist überall!" – oder wie man mit Mathematik die Welt verbessern kann
Unsere Welt wird ständig komplexer; technologische Entwicklungen und Digitalisierung schreiten rasant voran. Wie kann Mathematik dazu beitragen, die Herausforderungen unserer Gesellschaft zu bewältigen? Zum Beispiel mit effizienter Energieversorgung, nachhaltiger Mobilität oder personalisierter Medizin.
Mit diesen und weiteren Themen beschäftigt sich der Exzellenzcluster MATH+ und arbeitet dabei eng mit anderen Disziplinen zusammen. Durch kooperative Projekte mit Lebens- und Materialwissenschaften, Medizin, Physik und Informatik sowie Ingenieurs-, Geistes- und Sozialwissenschaften entstehen innovative Lösungen für dringende Zukunftsfragen.
MATH+ Forschende entwickelten Modelle, die die Ausbreitung der Römischen Kultur in Nordafrika beschreiben, halfen Archäologen, historische Straßennetzwerke auf Sardinien zu rekonstruieren, und simulierten gemeinsam mit Altertumswissenschaftler*innen und Geolog*innen, wie sich das Wollschaf nach einer Mutation im 6. Jahrtausend v. Chr. von Kleinasien aus verbreitete. Letztendlich könnten diese Modelle auch auf die Gegenwart angewendet werden, zum Beispiel bei der Frage, wie sich „Fake News“ und Nachrichten der sozialen Medien ausbreiten.
Berlin ist international bekannt für Spitzenforschung in anwendungsorientierter Mathematik. MATH+ hat das Ziel, Mathematik als Schlüsseltechnologie weiterzuentwickeln und ihre Anwendungen in Wissenschaft und Industrie zu stärken.
Schmerzmittel, die nicht abhängig machen, eine nachhaltige Verkehrsplanung, die Staus reduziert und Städte attraktiver macht, oder leistungsfähige Solarzellen zur Energieversorgung – das sind im Folgenden nur drei Beispiele aus der Forschung von MATH+, die das Potenzial der Mathematik verdeutlichen!
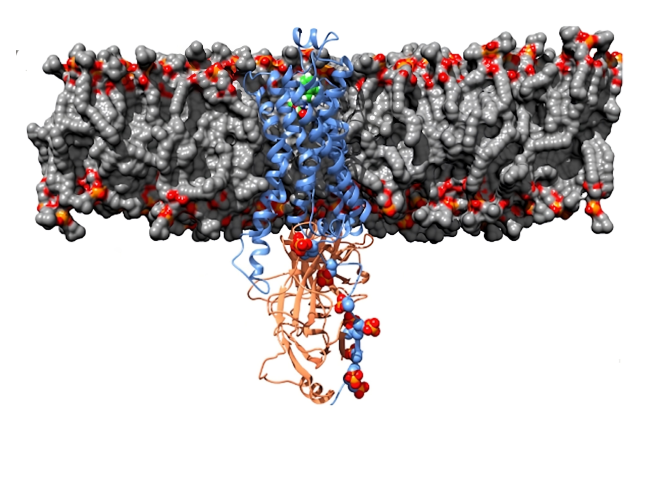
Wirkungsweise von Schmerzmitteln: Opioidrezeptoren (blau) sind in die Zellmembran (grau) eingebettet. Der Ligand, der Wirkstoff, der sich an den Rezeptor binden kann (grün), muss in den Rezeptor eintreten, um schmerzlindernde Effekte zu haben. © ZIB
Schmerzmittel mit weniger Nebenwirkungen durch mathematische Optimierung
Schmerzmittel haben oft schwerwiegende Nebenwirkungen oder bergen ein hohes Suchtpotenzial. Ziel der Wirkstoffentwicklung ist daher, Substanzen mit weniger Nebenwirkungen und geringerer Suchtgefahr bei mindestens gleicher Wirkung zu schaffen.
Forschenden von MATH+ ist mithilfe der Entwicklung neuer mathematischer Theorien und Algorithmen, die die Bindungsprozesse von Wirkstoffen an die Zielmoleküle präzise darstellen können, ein Durchbruch gelungen. Dies ermöglicht die genaue Berechnung der Bindungsraten eines Medikamentenkandidaten an den Rezeptor auf der Zelloberfläche, unter Berücksichtigung der chemischen Umgebung des Rezeptors. Da sich die chemische Umgebung zwischen gesundem und erkranktem Gewebe unterscheidet, wird die Entwicklung von Medikamenten möglich, die nur im erkrankten Gewebe wirken und so schwerwiegende Nebenwirkungen vermeiden.
Die Kombination aus mathematischer Innovation und moderner Wirkstoffforschung hat das Potenzial, die Medikamentenentwicklung sicherer und effektiver zu gestalten.
Ein FEM-Modell einer nanostrukturierten Solarzelle: mit der Finite-Elemente-Methode kann die Solarzelle in viele kleine Teile zerlegt werden, um ihre Eigenschaften und Funktionsweise genau zu analysieren und zu optimieren. © ZIB
Effizientere Solarzellen mit Hilfe von Mathematik
Bei der nachhaltigen Energieversorgung spielt die Nutzung von Solarenergie durch Photovoltaik eine zentrale Rolle. Mit Mathematik konnte der Wirkungsgrad von Solarzellen massiv gesteigert werden. MATH+ hat mit neuen mathematischen Modellen dazu beigetragen, die präzise Simulation der Wechselwirkung von Licht mit komplexen 3D-Strukturen zu ermöglichen. Diese Simulationen sind entscheidend, um das Material von Solarzellen auf molekularer Ebene zu verbessern. Künstliche Intelligenz und maschinelles Lernen werden genutzt, um die Eigenschaften dieser verbesserten Materialien vorherzusagen und so den Entwicklungsprozess weiter zu beschleunigen. Mithilfe der neuen mathematischen Erkenntnisse können Solarzellen entwickelt werden, die effizienter und leistungsfähiger sind und sowohl in kleinen elektronischen Geräten als auch in großen Solaranlagen eingesetzt werden können.
Interdisziplinäres Team erzielt Weltrekord
Ein spannendes Projekt in diesem Bereich ist das Helmholtz-Exzellenznetzwerk SolarMath, eine Kooperation zwischen MATH+ und dem Helmholtz Zentrum Berlin. Physiker*innen und Mathematiker*innen arbeiten gemeinsam an der Verbesserung der Effizienz von Solarzellen. Gemeinsam haben sie monolithische Perowskit/Silizium-Tandem-Solarzellen mit Wirkungsgraden von knapp 30 Prozent entwickelt – ein Weltrekord! Durch ihre verbesserte Oberflächen nutzen diese Solarzellen das volle Spektrum der Sonnenstrahlung, wodurch ihre Effizienz erheblich gesteigert wird.
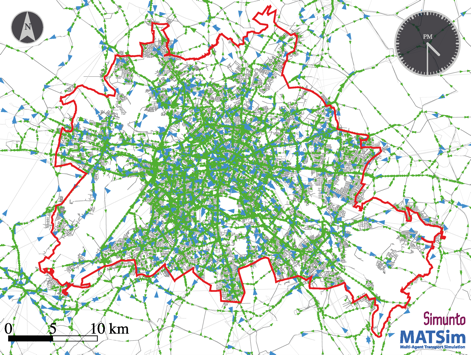
Ausschnitt aus einer Simulation des Individualverkehrs (grüne Fahrzeuge) und des öffentlichen Verkehrs (blaue Fahrzeuge) in Berlin. © TU Berlin, VSP
Optimale Verkehrsplanung mit mathematischen Simulationen
Individualverkehr treibt den Klimawandel an, aber gleichzeitig ist er von enormer Bedeutung für die Wirtschaft. Deshalb besteht ein dringender Bedarf an effizienten und nachhaltigen Transportsystemen.
Die Lösung dieser komplexen Probleme erfordert innovative mathematische Ansätze. In ihnen werden Algorithmen für dynamische Netzwerkflüsse mit sogenannter agentenbasierter Verkehrssimulation und Modellen, die eine präzise Simulation des realen Verkehrs ermöglichen, kombiniert (MATSim – Multi-Agent Transport Simulation Toolkit, mitentwickelt von MATH+). Simulationen helfen auch, die bisherige Verkehrspolitik zu bewerten und zukünftige Systeme zu planen. So könnten mit MATSim beispielsweise die Effekte zeitabhängiger Mautgebühren ermittelt werden.
Konsequenzen abwägen in Echtzeit
Ergänzt wird diese Forschung durch sogenannte "Decision Theatres", in denen Schulklassen, gesellschaftliche Interessensgruppen und Entscheidungsträger*innen Mobilitätsoptionen und deren Vor- und Nachteile diskutieren. Grundlage für die Decision Theatres ist das Mobility Transition Model MoTMo, das mit agentenbasierter Modellierung arbeitet. Die Ergebnisse bieten eine fundierte Grundlage, um die Verkehrsnetze der nächsten Generation gestalten zu können.